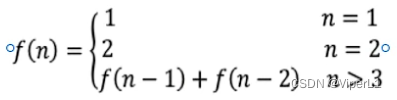一、基本概念和术语
1、算法复杂度
复杂度分析: 事后统计法 大0表示法:T(n)=O(f(n))
2、时间复杂度分析
只关注循环次数最多的一段代码
总复杂度等于最高阶的复杂度
嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
推导大O阶
1.用常数1代替运行时间中的所有加法常数项
2.仅保留最高阶
3.若最高阶项存在且不为1,则将其系数取1
常见时间复杂度
| 常数阶 O(1) | int i =1(无循环结构) |
| 对数阶 O(log2n) | while{ i = i * 2 ;} (while循环,不线性递增) 底为其递增步长 |
| 线性阶 O(n) | for(i=1;i<=n;++i) {j++;}(for循环,线性递增) |
| 线性对数阶 O(nlogN) | for+while (本质是n * logN) |
| 平方阶 O(n^2) | for嵌套 |
| K次方阶 O(n^K) | for的K次嵌套 |
二、递归思想
1.一个问题的解可以分解为几个子问题的解(自我调用)
2.这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样
3.存在基线/终止条件
缺陷:1.空间复杂度高;存在溢出风险;调用较为耗时;存在重复调用问题
大部分递归可以转换为循环
三、爬楼梯问题
假设你正在爬楼梯,需要n阶才能达到楼顶,每次你可以爬1~1个台阶,你有多少种不同的方法爬到楼顶?
解题思路:若第一次走了一步,那解决方法就等于1+剩下的可能,依此类推
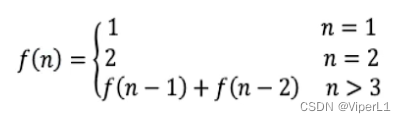
终止条件:f(1)=1,f(1)=2均为终止条件
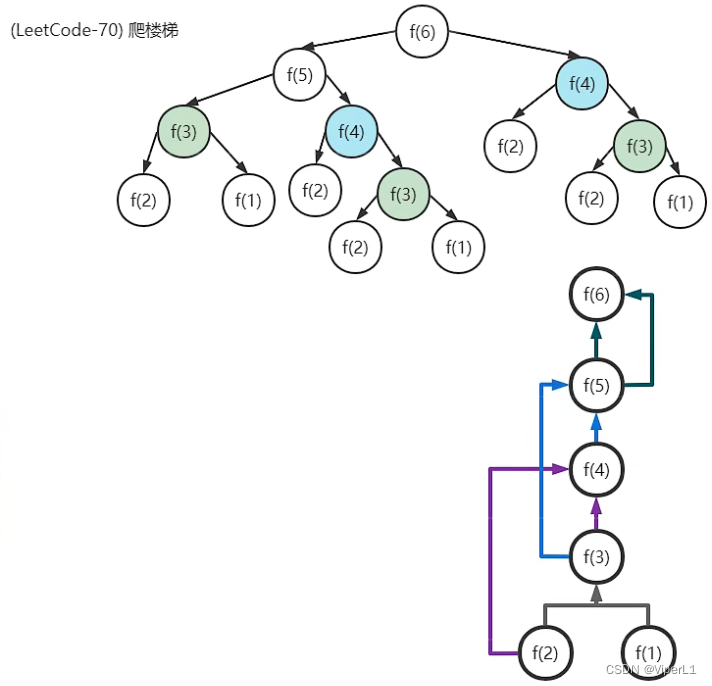
public int Climb(int n)
{
if(n==1) return 1;
if(n==2) return 2;
return Climb(n-1)+Climb(n-2);
}循环解法,自底向上累加
public Climb()
{
if(n==1) return 1;
if(n==2) return 2;
int result = 0;
int pre = 2;
int prePre = 1;
for(int i = 3; i<=n;++i){
result = pre + prePre;
prePre = pre;
pre = result;
}
return result;
}